Statystyka to ważny dział matematyki. Co można z niej „wycisnąć” pokazał w ciekawym tekście Andrzej Graf, prywatnie mój szwagier, a zawodowo pracownik Urzędu Statystycznego. Wszystko poparte obliczeniami. Zainteresuje to na pewno wszystkich kibiców piłki nożnej, niecierpliwie oczekujących na losowanie grup i mistrzostwa.
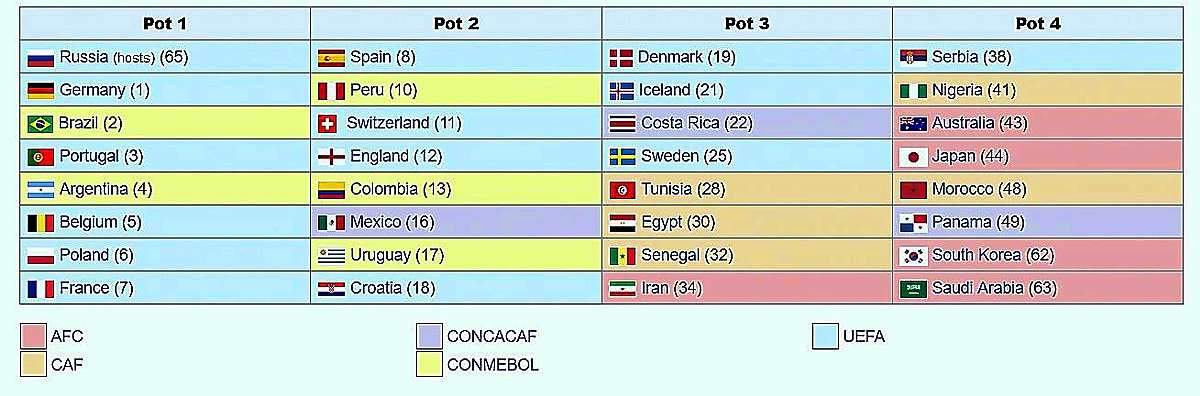
Chciałbym z punktu widzenia matematyczno-statystycznego przeanalizować jakie są szanse trafienia przez reprezentację Polski w piłce nożnej poszczególnych przeciwników w losowaniu mistrzostw świata w piłce nożnej, które odbędzie się w najbliższy piątek 1 grudnia w Moskwie. Jak wiemy 32 uczestniczące zespoły zostały podzielone na cztery koszyki po 8 drużyn każdy na podstawie rankingu FIFA wg stanu z października br. Dzięki temu zestawieniu Polska znalazła się w pierwszym koszyku wraz z Rosją, Niemcami, Brazylią, Portugalią, Argentyną, Belgią i Francją. Tym samym tych reprezentacji nie wylosujemy w pierwszej-grupowej rundzie mistrzostw.
Na kogo możemy trafić? Otóż zostanie do nas dolosowany jeden zespół z każdego z pozostałych koszyków (drugiego, trzeciego i czwartego). Ile mamy kombinacji tj. możliwych wariantów grup z udziałem Polski? Na początek to proste, mnożymy liczbę zespołów w drugim koszyku przez liczbę drużyn w trzecim i czwartym koszyku, czyli 8 x 8 x 8 i otrzymujemy 512 kombinacje. Sprawę komplikuje kolejny warunek według którego będzie przeprowadzone losowanie. Podobnie jak w poprzednich edycjach mistrzostw, żadna grupa nie może mieć więcej niż jednego zespołu z tej samej konfederacji kontynentalnej, z wyjątkiem Europy, z której mogą być najwyżej dwa zespoły w grupie. Założenie to powoduje, że liczba wariantów grup na które może trafić reprezentacja Polski dość znacznie zostaje zmniejszona, jak wyliczyłem z 512 na 282. To jednak ciągle dużo i oznacza, że prawdopodobieństwo wylosowania danej grupy wynosi 0,35 %.
Z punktu widzenia rachunku prawdopodobieństwa wylosowanie z każdego koszyka, np. Hiszpanii z drugiego zestawu jest takie same i wynosi jeden do ośmiu. Jednak przyjęty warunek separacji drużyn z tych samych konfederacji powoduje, że do końca tak nie jest. W praktyce, bazując na sposobach losowań poprzednich edycji będzie wyglądać to tak, że jeżeli do grupy B z pierwszego koszyka zostanie wylosowana Brazylia, a do grupy C Polska, to przy wylosowaniu z drugiego koszyka do gr.B – Peru, zespół ten trafi jednak do grupy C z Polską, ponieważ nie może grać w jednej grupie z Brazylią.
Przechodząc do możliwości wynikających z 282 dopuszczalnych kombinacji to z drugiego koszyka najwięcej wariantów przewiduje, że reprezentacja naszego kraju spotka się z którymś zespołów z Ameryki Południowej, tj. z Kolumbią, Peru lub Urugwajem (50 wariantów na każdy zespół, co stanowi 17,7%, czyli łącznie ponad 53 % za Ameryką Południową). Na zespoły z Europy, które raczej chcielibyśmy ominąć na tym etapie np. Hiszpanię czy Anglię przypada 8,5% ogółu możliwości.
Z koszyka trzeciego, statystyka przewiduje największą szansę dla Polski na grupę z udziałem Kostaryki (45 wariantów i 16,0%), a z ostatniego teoretycznie najsłabszego koszyka czwartego na grupę z udziałem którejś drużyny z Azji, tj. Arabii Saudyjskiej, Japonii, Korei Południowej lub Australii (43 warianty i 15,2%), czyli łącznie 60,8% wariantów za Azją. Tak na marginesie to nie pomyłka, w FIFA Australia należy do konfederacji azjatyckiej.
Podsumowując, takie statystyczne losowanie byłoby dla nas dość przychylne. Uniknęlibyśmy, przynajmniej na początek, teoretycznie najsilniejszych zespołów. Osobiście i bazując na powyższej analizie stawiam na grupę POLSKA, PERU, KOSTARYKA, ARABIA SAUDYJSKA. Co ciekawe z każdym z tych zespołów na przestrzeni dziejów naszej reprezentacji dotychczas potykaliśmy się trzykrotnie odnosząc komplet 9 zwycięstw, przy czym z Peru graliśmy też w finałach mistrzostw świata w roku 1978 i 1982, a z Kostaryką w roku 2006!
Życzę przyjemnej zabawy w typowanie składu naszej grupy na mistrzostwach świata w piłce nożnej pamiętając, że z punktu widzenia rachunku prawdopodobieństwa każda z 282 kombinacji ma takie samo prawdopodobieństwo zaistnienia.